Introduction
This research is done in 2 parts, the first being the concept of game theory - this will mainly focus on the originality of game theory, its main definition including a specific example I've come up with an example to show you how it all applies to blockchain. Lastly, we'll finish off our analysis by providing a short description of what blockchain is and how we'll apply our previous example to build an app using the solidity framework.
What is Game Theory?
Game theory is the study of mathematical models to strategize decision driven scenarios, these scenarios are essentially interactions between rational decision-makers. Rational decision-makers are "players" which play a significant role in the overall "game". Each player can either influence the decision of the other and can even influence the outcome of such a decision. Which in turn can play out a set of different occurrences in our every daily life including politics, business, banking, and even voting. With endless possibilities comes different outcomes in such "games", and a slew of different scenarios that constitute a solution.
Proof of Enactment
To get a better understanding of Game Theory I've come up with an example involving a cooperative game where members pay a subscription fee to be part of a community and can cast a vote on various agreements that are placed by the organization. These organizations can create a "poll" inside the community forum and depending on the result, they must abide by whatever the outcome of the "poll" result may be. This situation has various outcomes but we will focus on four important ones. The options in which the scenarios can end up being...
1. Organizers can choose to not fulfill the intended result from the vote.
2. Organizers can fulfill the request based upon the outcome of the vote.
3. Voters can decide to do nothing.
4. Voters can decide to verify the organizer.
Process Description
Each "game" comes with a set of decisions that need to be executed by the players, in this case, we have two players the "Organizer" and "Participant". Depending on the behavior of each player there will come an outcome that determines the player's payoff. The table below shows what is called a variable-sum payoff matrix, this allows us to properly align the player's payoff depending on how much value it gets from playing. We must require this process to deduce one from another, in our case we layout both players on the side and place the payoffs in the middle. The Organizer up top has four choices depending on how the Participants (Voter) respond and vice versa.
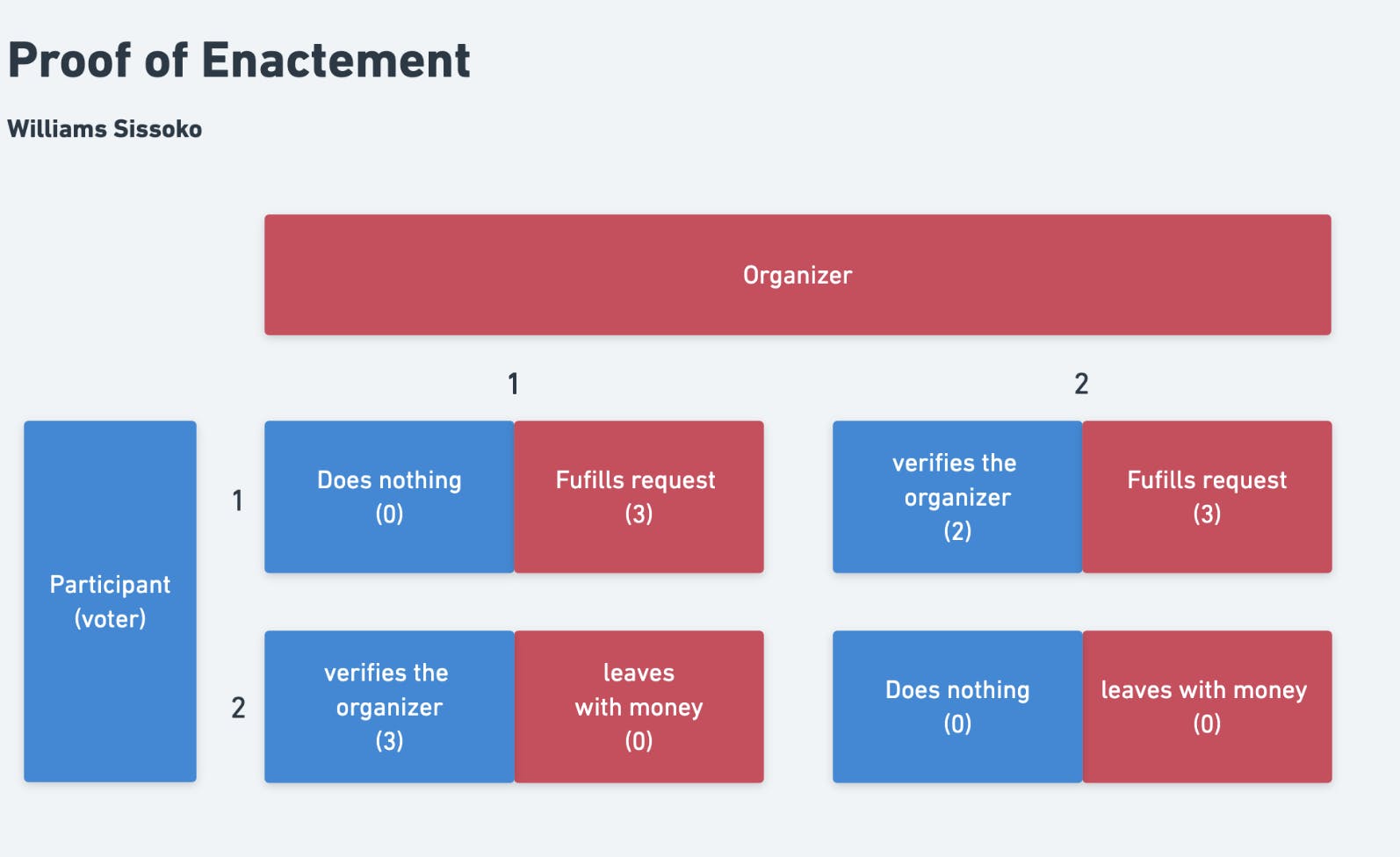
The Organizers
In the example above I've designed the game to incentivize both players to participate inside the "game". To ensure both players cooperations we must apply points as an advantage mechanism that incentives the organizer or the Participant (Voter) to play and choose the most "sure thing" principle to maximize its payoff by determining the minimum it will take. Thus, the Organizer must choose between "fulfilling the request" and "leaving with the money" as we can see from the diagram it is in his best interest to fulfill the request from the voter or suffer the consequences.
The Participants (Voters)
As for the participants (voters), it has two choices "do nothing" or "verify the organizer" as we must incentives the game to ensure both players lose if they don't participate we can see that if the voter decides to do nothing when the organizer decides not to fulfill the request then we must keep the participant (voter) accountable by applying some sort of consequence to the participant (voter).
Cost Benefit-Analysis
Now we'll describe the cost-benefit analysis for both players that can be explained through the Nash Solution (John F Nash - American Mathematicians who pioneered the Nash equilibrium and his work related to game theory). By applying a balanced threat we ensure that no agreement is reached between both players which in turn ensures that both players suffer some sort of defeat (Davis 2020), in our case, it will be if a player does not participate. The game is designed to ensure that both parties suffer if they do not participate now we must apply a real-world scenario of such outcomes in our game.
The Participants (Voters)
Participant (Voter) has a specific duty in this game and that is he does nothing he will ultimately lose. This means that the process in participation points comes from the verification process the voter must complete to ensure that the organizer is held accountable. We then reward every voter for their verification process with a token and none if they do not participate.
The Organizer
As for the Organizer they must be held accountable for not fulfilling the voter's request, to ensure that they don't leave with the voter's money we will apply a two-step process where the organizer must require a "Proof of Enactment" based upon each voting result. If the Organizer chooses not to fulfill the request two actions will happen:
The money will return to the voter accordingly (The voter's subscription fee for that specific month)
The organizer will be placed in a warning zone and given one more chance to ensure the voter's trust or else face being kicked out of the game.
Thank you for reading :)
I hope you've learned something here because I for sure did! Next week we'll explore how we will apply this into code using solidity and design a contract based upon this scenario I've come up with. Thanks for reading and I welcome any sort of feedback as I took what I sort of learned in class and with additional research applied it into my examples. 🥳
Resources
https://arxiv.org/pdf/1902.10865.pdf#:~:text=Game theory provides a set,given the other players'%20strategies.&text=blockchain%2C%20players%20can%20be%20miners,pools%2C%20or%20the%20blockchain%20users.

